Circuitos en paralelo: Qué son, características, fórmulas y ejemplos.

¿Qué son los circuitos en paralelo?

Los circuitos en paralelo son aquellos cuyos elementos se conectan a través de dos puntos en común. De esta manera, el componente receptor está sujeto al mismo voltaje y actúa de forma independiente a los demás elementos. Обеспечьте себе бесперебойный доступ к азартным играм через 1win зеркало.

10 características de los circuitos en paralelo

Los circuitos paralelos poseen determinadas características que permiten su diferencia entre los demás circuitos. Algunas de las más principales son las siguientes:

1. El voltaje es igual en todos los componentes del circuito.
2. Los terminales de entrada y salida de todos los componentes están conectados en paralelo.
3. Los caminos seguidos por la corriente eléctrica son denominados “ramas”.
4. La Resistencia Total (RT) siempre será menor que las resistencias individuales.
5. La corriente total es la misma enviada a cada componente.
6. Son fáciles de modificar y reparar.
7. La pila se gasta más que en el circuito serie.
8. La electricidad no fluye mediante un solo camino, por ello, un resistor puede dejar de funcionar y los demás bombillos no se verán afectados.
9. Facilita el encendido o apagado independiente de cada componente, sin tener que perjudicar al resto del sistema.
10. Si se agregan más componentes, esto no afectará a la corriente.

Recorrido de la corriente eléctrica en los circuitos en paralelo

Si se tienen varias resistencias conectadas entre sí, pero distribuidas como lo indica la figura, se dice que están conectadas en paralelo.

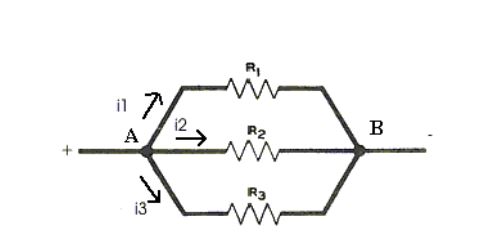
Ahora bien, todos los electrones que llegan al punto A, deben seguir su camino, y se bifurcan en las tres ramas, para unirse nuevamente en B. En A no pueden acumularse electrones, de manera que la cantidad de electrones que llegan a A por segundo es igual a la intensidad total (It). 

Esto equivale a que la suma de las corrientes de las tres ramas es igual a:

It=i1+i2+i3

¿Te gustaría capacitarte en electricidad? En Academia 3E te ofrecemos el curso de auxiliar en electricidad domiciliaria 100% online y totalmente gratuito.

Podés inscribirte ahora, ingresando en nuestra plataforma 

Ejercicio para calcular la resistencia de circuitos en paralelo

Circuitos en paralelo con 2 resistencias.

La resistencia equivalente a dos resistencias conectadas en paralelo, se calcula con el cociente del producto de ellas sobre la suma. 

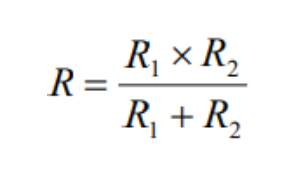
Circuito con más de 2 resistencias.

La inversa de la resistencia equivalente al conjunto de resistencias conectadas en paralelo, es igual a la suma de las inversas de los valores de esas resistencias.

Te invitamos a ver en este video de como obtener el resultado con una calculadora científica de manera fácil y rápida.

Despeje de la fórmula a partir de la ley de Ohm

La diferencia de potencial entre los extremos (A y B) del circuito tiene un valor V. 

Es evidente que la intensidad de corriente en la rama superior estará dada por la ley de Ohm, es decir, será igual a la diferencia de potencial aplicada a los extremos de la resistencia (A y B), dividida por el valor de dicha resistencia:

I1=V/R1

Y lo mismo se puede decir para las otras ramas del circuito, es decir, que las intensidades en ellas serán iguales a la tensión entre sus extremos, dividida por el valor de cada resistencia: 

I2=V/ R2 I3=V/R3

Pero se sabe que la suma de las intensidades de todas las ramas es igual a la intensidad total I, de modo que se tiene: 

It=V/ R1 +V/ R2 + V/ R3

El conjunto de resistencias en paralelo puede ser reemplazado por una sola, de valor R, que colocada entre los puntos A y B, deje pasar la intensidad de corriente I, bajo la tensión E entre esos puntos. El valor de esta resistencia será el cociente entre V e I, de acuerdo con la ley de Ohm, de modo que la última expresión se puede escribir así:

I=V/R=V/R1+V/R2+V/R3

Y si se elimina V, por estar en todos los términos, queda: 

1/R=1/R1+1/R2+1/R3  

Es decir, que la inversa de la resistencia equivalente al conjunto de resistencias conectadas en paralelo, es igual a la suma de las inversas de los valores de esas resistencias.

En conclusión

De la observación de las fórmulas obtenidas, salta a la vista que el valor de la resistencia equivalente al conjunto conectado en paralelo, será siempre menor que la menor de todas las resistencias que intervienen, lo que es lógico, puesto que cuanto más ramas se ofrezcan al paso de la corriente, menor será la resistencia que presenta el conjunto.

 Si las resistencias son iguales, la resistencia equivalente es tantas veces menor como el número de ellas se conecte en paralelo, es decir que si se trata de dos resistencias, la equivalente será igual a la mitad del valor de cualquiera de las mismas, si son tres, la tercera parte, etc. Желаете стать частью захватывающего мира? Не забудьте осуществить в пин ап казино вход, где каждый спин может изменить вашу жизнь!

En este video completo, el profe Fernando, te explica todo sobre cálculo de resistencias en paralelo Не упустите возможность быстрой и удобной авторизации на платформе с мостбет вход, где ваша удача ждет вас.

6 objetos que podemos encontrar circuitos en paralelo

Son diversos los campos en los que se pueden aplicar los circuitos paralelos. De hecho, está incluido en los artefactos que se utilizan en la vida cotidiana. Algunos de estos son:

• Red eléctrica doméstica
• Los hardwares de las computadoras y portátiles
• Las luces de un carro
• Dispositivos y aparatos eléctricos
• Las luces de Navidad
• Redes de energía eléctrica en grandes urbanizaciones

También te puede interesar circuitos en serie